When ancient people began to count, they used their fingers, pebbles, marks on sticks, knots on a rope and other ways to go from one number to the next. As quantities increased, more practical representation systems became necessary.
In different parts of the world and at different times, the same solution was created: when a certain number is reached, a different mark is made representing all of them. This number is the base. Units continue to be added until the previous number is reached for the second time and another mark of the second class is added. When a given number (which may be different from the former being the auxiliary base) of these second order units is reached, a third order is added and so on.

In this article, we will describe the different kinds of numeral systems that ancient civilizations and cultures have used throughout history.
Ancient Civilizations Numeral Systems
Hebrew Numeral System
The Hebrew numbering system is an alphabetic quasi-decimal system in which the letters of the Hebrew alphabet are used. It as a non-positional system which relies on 22 symbols, but none of them is used to represent zero.
Babylonian Numeral System
This system appeared for the first time around 1900-1800 B.C. in Babylon, which was a city of lower Mesopotamia and was located in what is today Iraq. It is the first numbering system which is positional, which has 60 as its base, and they had a separate sign for zero.
Egyptian Numeral System
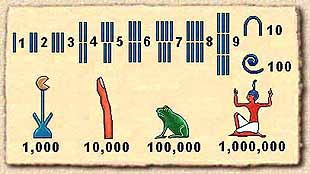
From the third millennium B.C. the Egyptians used a system to write numbers in base ten, utilizing hieroglyphics to represent the order in which the units with which they were working were grouped. The Egyptian numeral system was decimal and not positional, and they used a symbol to represent zero.
Roman Numeral System
The Roman numeral system is a non-positional system of numbering which was developed in Ancient Rome and was used in all the Roman Empire, it is calculated that it arose by 480 B.C. In the Roman numeral system, no symbol exists to represent the value zero, it is of a base ten type and utilizes seven symbols.
Chinese Numeral System
The classical form of writing numbers in Ancient China began to be used from approximately 1500 B.C. onward. It is a strict decimal system which uses the units and the distinct capabilities of 10. They did not use a symbol for zero and it is of a positional character.
Mapuche Numeral System
The Mapuche people developed a culture of rich oral tradition, because of which their system of numbering was represented through words. The principles which the Mapuches utilized were:
a) Additive: a number placed to the right of 1, 10, or 100 adds to these its value. For example, “mari regle” is 10 + 7 = 17.
b) Multiplicative: a number placed to the left of 1, 10, or 100 multiplies these by its value. For example, “kula warangka” is 3 x 1 = 3.
It is a base ten, non-positional system of numbering which does not use a symbol for zero.
Greek Numeral System
It was a system with a decimal base which does not have a symbol for zero and was based on a summative principle. In order to represent a unit and the numbers up to 4, they used vertical lines. For 5, 10, and 100 the letters corresponding to the initial of word five (pente), ten (deka), and a thousand (khiloi). For this reason this system is called acrophonic.

Aztec Numeral System
This numeration is based on the additive principle according to which the value of a representation is obtained by adding the values of the figures. It was a numeration with a vigesimal base (20). In Mexico between the 14th and 16th Centuries or our era the Aztec civilization developed; these developed their own system of numeration. The numerical system employed had a vigesimal base and is a partitive system of numbering.
The Incas developed a way of registering quantities and representing numbers through a decimal, positional numeral system: a group of cords with knots which were denominated quipus (“khipu” in Quechua: knot).
Ionic Numeral System
Quasi-decimal alphabetic system, sometimes called Ionic (it is an improvement on the ancient Greek system). To each figure of a unit (1-9) a letter is assigned, to each ten (10-90) another letter, and to each hundred (100-900) another letter. A sharp accent is placed at the end of the group to distinguish numbers from letters.
Attic Numeral System
Attic numeration was used by the ancient Greeks, probably starting in the 7th Century B.C. It is the oldest system of those employed by the Greeks. They were also known as Herodianic numbers, as they appear described for the first time, in a manuscript by Herodian from the 2nd Century. It is a base ten system of numbering, which is positional but does not use a symbol for zero.
Maya Numeral System
The Maya civilization arose at the end of the 14th Century B.C. The Mayas came up with a base 20 system, with 5 as an auxiliary base. The Maya civilization was the first in America to think up the zero. This was necessary for their numeration because the Mayas had a positional system and there were only three symbols to represent numbers.

Arabic Numeral System
The Arabic numbers originated in India at least 1,700 years ago. It is a system of a decimal type (base ten), which has a symbol for zero and utilizes 9 symbols. The world owes the transcendental invention of the base ten system of numeration, called positional, to the Indian culture. The “Arabic” system has been represented (and is represented) using many different groups of glyphs.
Types of Numeral Systems used in History

Decimal Numeral System
This system was developed by the Hindus. It is not known with any certainty exactly when the invention of this system happened, but it is supposed that it was between the 2nd and 6th Centuries A.D., but it was not until the 12th Century that they were introduced in Europe. It is a positional system of numeration in which quantities are represented using the number ten as a base. It uses ten symbols, and does have a symbol for zero.
Binary Numeral System
The ancient Hindu mathematician Pingala presented the first known description of a binary system of numeration in the third century. The Binary system of numbering utilizes only two digits, the zero and one. The binary system uses positional notation.
The binary or base 2 numeral system is a positional system which uses only two symbols to represent a number: 1 and 0.
Unary Numeral System
It is a base 1 numerical system. It has symbols for 1, 10, 100, 1000, 10000, 1000000, up to 1000000000. It does not use the zero and is positional. The traditional system of counting on fingers is an example of unary numeration. The unary system is useful in processes of counting, like the scoreboard in a sport, or counting the number of people who enter a place, or the number of votes going out in an election, as it does not require amending previous results, only that one keep adding symbols for the later recount.
Quinary Numeral System
It is base 5, and utilizes the digits from 0 to 4. It is positional. It was developed based on the fact that humans have five fingers on each hand. It is one of the most ancient systems of numbering, also being the name of an ancient Roman coin of the same value.
Hexadecimal Numeral System
Base 16 system, introduce in the field of computation for the first time by IBM (International Business Machines) in 1963. It is a system of numeration which employs 16 symbols which, according to the general theorem of positional numeration, equal the number in base 16, two hexadecimal digits correspond exactly to one byte.
Octal Numeral System
The base 8 numerical system is called octal and utilizes the digits 0 to 7. To convert a number in decimal base to octal base, it is divided by 8 successively until reaching a quotient of 0, and the remainders of the divisions in inverse order indicate the number in octal. To go from base 8 to decimal base, one only has to multiply each figure by 8 elevated to the position of the figure, and add the results.
